最近在爬文的時候，經常看到樹Tree這個資料結構，像是MySQL使用的B+樹、Java HashMap、C++ Map使用的紅黑樹，還有很常聽到的二元樹、二元搜尋樹、AVL樹、霍夫曼樹等等…
雖然在大二的時候有修過資結，但因為缺乏實際使用與了解，所以對樹還是比較陌生，因此這幾天又花點時間來複習，同時也整理一下學習的筆記。

本文適合像我一樣對樹的概念還不是那麼熟悉的朋友閱讀，可以算是對樹的概述，因此不會具體介紹每種樹的相關演算法(新增、刪除、查詢、平衡…)，而是簡單的介紹每種樹的結構與要解決的困難，讓你可以快速對常見的樹建立起基本的認識。

簡介

什麼是樹

樹是由>=1個節點(Node)相互連接組成，並且會有一個樹根節點(Root)，而其餘節點也都可以形成一個樹狀結構。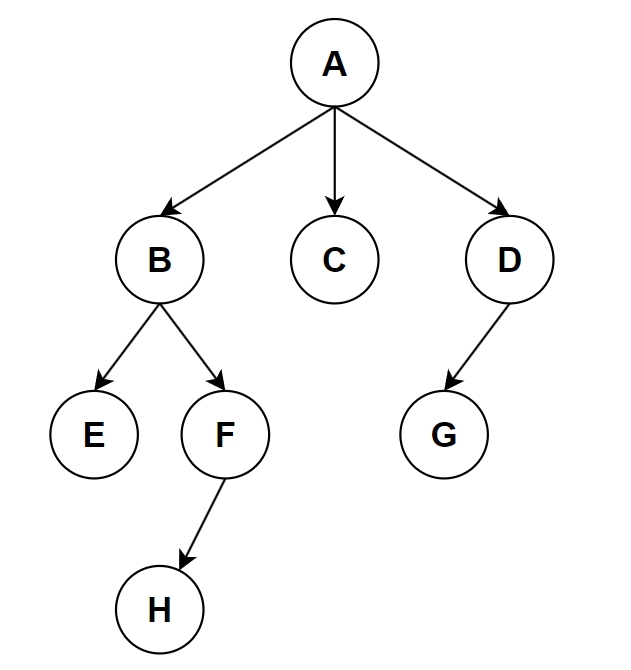

使用樹的好處

一般我們在查詢線性結構，如陣列(Array)或是鏈結串列(Linked List)中的元素時，需要走訪每個節點，因此時間複雜度是O(n)，但如果使用樹狀結構的話，在好的情況下(樹平衡時，這後面討論)可以只需要花費O(logn)的時間就能找到目標元素，因此使用樹的優勢就是擁有快速的查詢性能。
除此之外，因為通常樹會使用Linked List儲存，因此新增與刪除節點的操作也非常方便快速，只需要修改指向的記憶體位置即可，給予我們很大的靈活性。

樹的應用

樹的應用非常廣泛，像是Windows的檔案系統、資料庫系統、人工智慧和機器學習中的決策樹等方面，都可以看到樹的蹤跡。

常用術語

  • Parent父節點：連接上一層的節點
  • Child子節點：連接下一層的節點
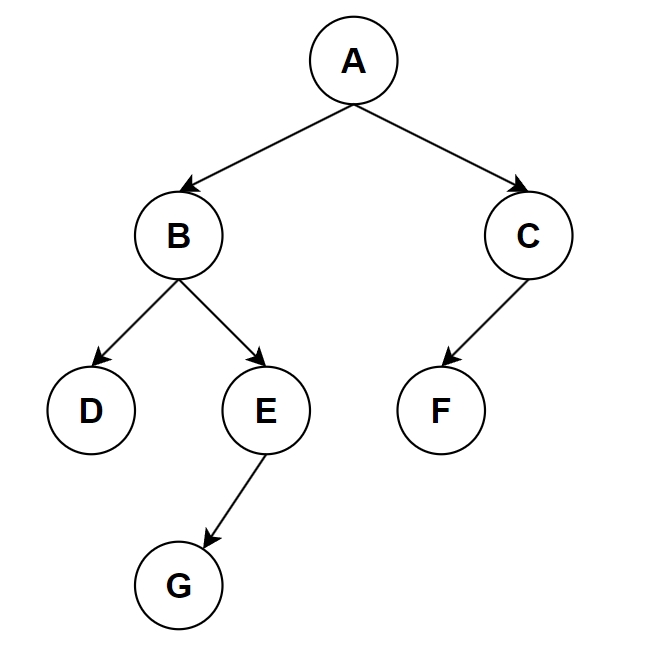
  • Degree分支度：一個節點有幾個子節點。如：A的分支度為3，B的分支度為2，C的分支度為0。
  • Root根節點：最上層的節點
  • Leaf樹葉節點：沒有子節點(分支度為0)的節點
  • Height高度：樹總共有幾層

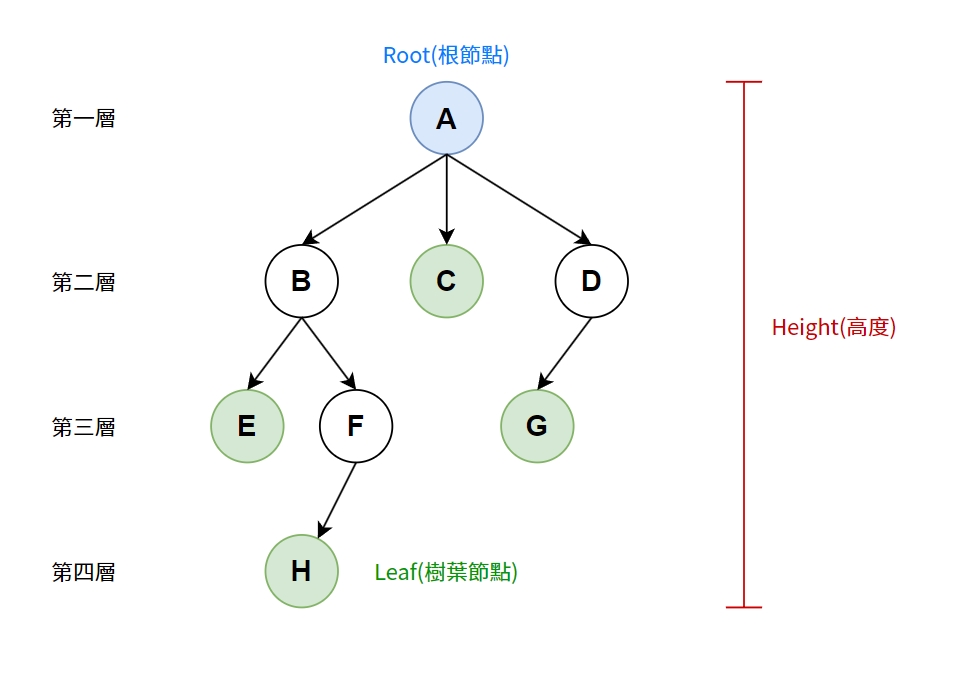
電腦中如何儲存樹

我們可以使用一維陣列或是Linked List來儲存，通常會使用Linked List，優點是方便新增刪除節點，缺點是比較不好找到父節點。

二元樹

n元樹有什麼問題

前面有提到，一般存放樹會使用Linked List，因此對於一個最大分支度為n的樹(n元樹)來說，每個節點就需要分配長度n+1的空間存放該節點的資料與指向的子節點的指標。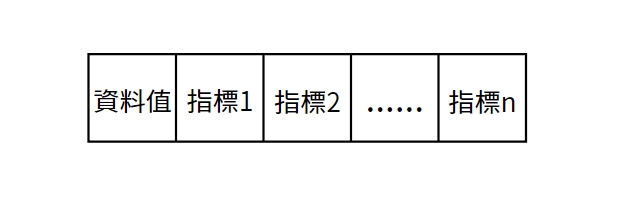

而當n越大時，就越容易造成空間浪費(下圖空白區域)。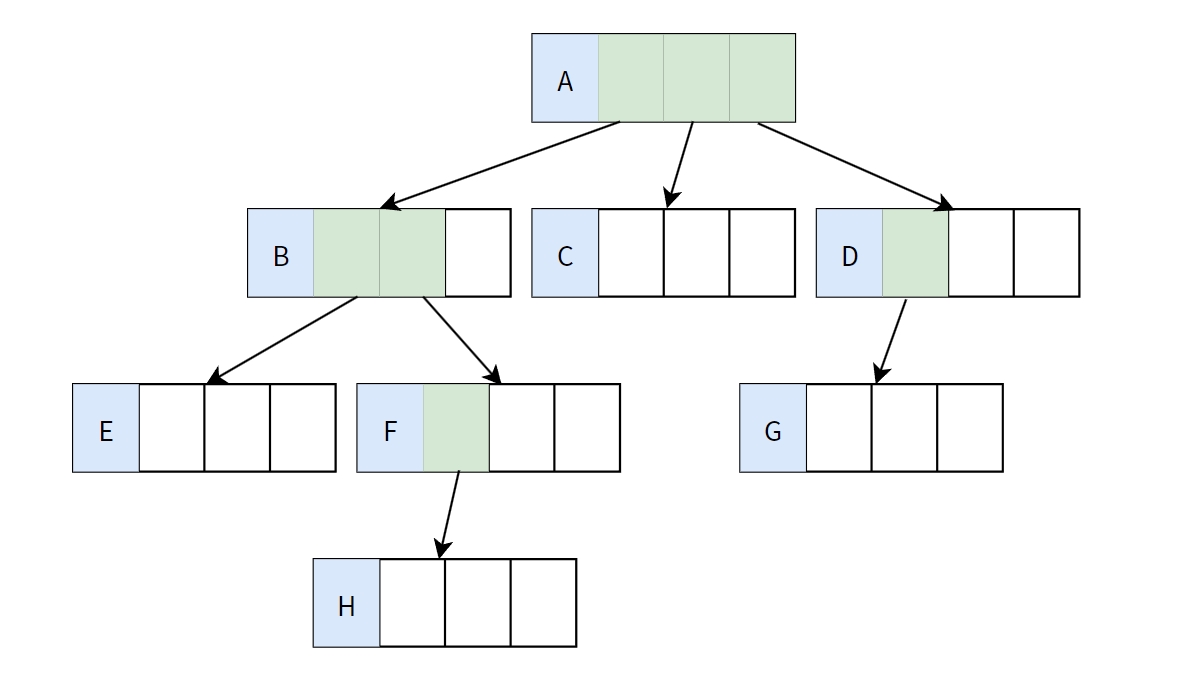

因此如果要節省空間，最好的方法就是使用二元樹，即分支度<=2、最多只能有2個子節點的樹。

定義

  1. 有根節點、左子樹、右子樹
  2. 左右子樹也要是二元樹

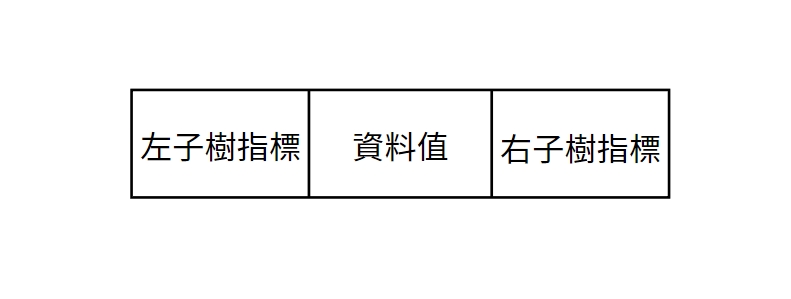
二元搜尋樹

定義

也是一種二元樹，但需要額外滿足以下條件：

  1. 左子樹的值 < 根的值 < 右子樹的值
  2. 左右子樹都要是二元搜尋樹
  3. 沒有重複的值

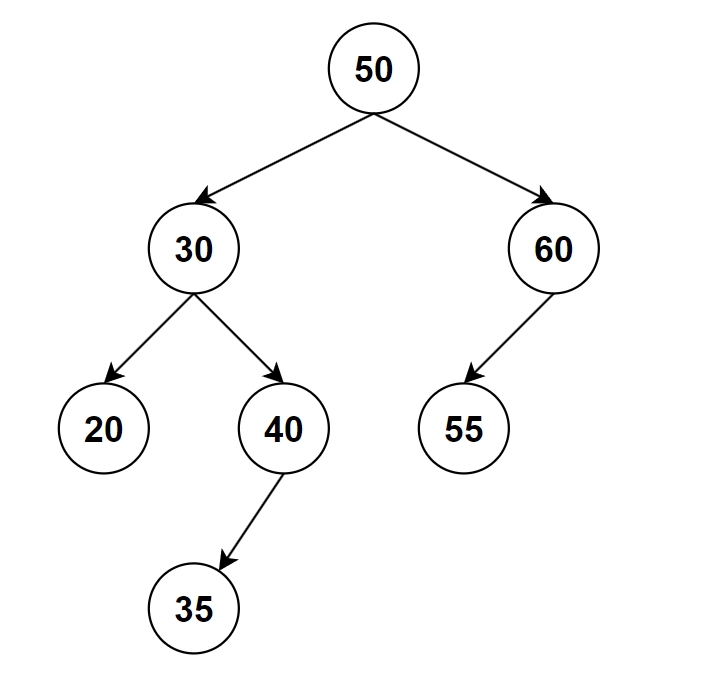
優點

因為二元搜尋樹會將元素值按照大小排序，小於根的值往左邊放，大於根的值往右邊放，這樣的特性讓我們可以在搜尋時，每次與根的值比較後，就會縮小一半的搜尋範圍，提升搜尋的速度，時間複雜度是O(logn)。

自平衡二元樹

當我們對二元搜尋樹新增或刪除節點時，往往會導致樹不平衡，如果很不幸的，我們的二元搜尋樹變成了左右極度不平衡的二元樹，甚至是歪斜樹(完全沒有左節點或右節點的二元樹)的話，這樣搜尋方式就跟Linked List一樣是每個節點走訪，時間複雜度就會退化為O(n)，這很顯然不是我們要的。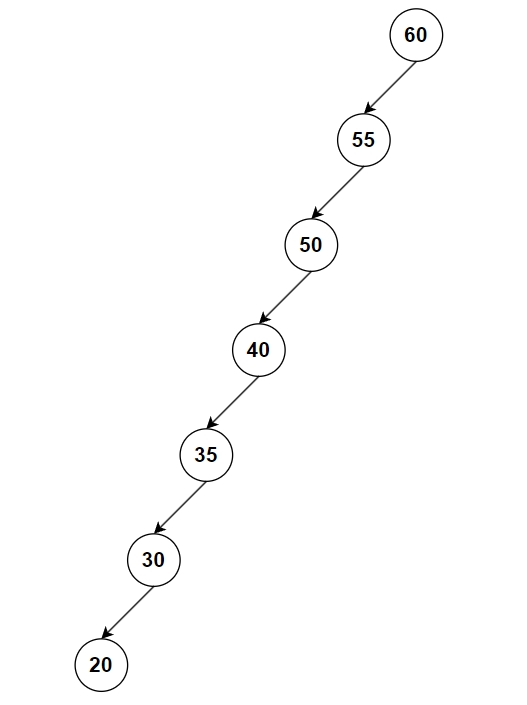

而為了解決這個問題，就有了自平衡二元樹的出現。
自平衡二元樹在每次新增刪除後，會自動檢查是否平衡，不平衡的話就要通過一系列旋轉操作，調整回平衡的狀態，具體過程這裡我就不多贅述了，感興趣的朋友可以參考其他書籍或文章。
以下介紹AVL樹與紅黑樹兩個經典的自平衡二元樹。

AVL樹

定義

  1. 左右子樹的高度差<=1
  2. 左右子樹都也要是AVL樹

優點

AVL樹是一個嚴謹的自平衡二元樹，隨時都保持高度平衡，因此查詢的效率非常快，適合用在頻繁讀取的場景。

缺點

為了要保持高度平衡，AVL樹會在每次新增刪除過後，透過較多次旋轉操作恢復平衡，所以在這裡效能消耗會多一些。

紅黑樹

定義

  1. 每個節點只能是紅色或黑色
  2. Root根節點一定是黑色
  3. Leaf葉節點一定是黑色(紅黑樹的葉節點是NIL節點)
  4. 紅色節點的兩個子節點一定是黑色 (不能有兩個紅色節點相連)
  5. 從任一節點出發到葉節點所有路徑的黑色節點數目要相同

(這個規則其實是從2-3-4樹過來的，算是比較深入的內容，有興趣的朋友可以到图解：什么是红黑树？看看)

圖片來自維基百科-紅黑樹

優點

紅黑樹是一個較寬鬆的自平衡二元樹，不要求高度平衡，只有在滿足條件的情況下才會調整，因此所需的旋轉次數較少，適合用在頻繁新增刪除的場景。

缺點

因為紅黑樹結構相對鬆散，所以查詢效率不及AVL樹。

應用

紅黑樹在新增、刪除、查詢的效率都非常快速與穩定，因此適用於大多數場景，許多程式語言也會使用紅黑樹實作各種容器，像是Java的HashMap、C++的Map等等。

B樹

自平衡二元樹中，一個節點只能存放一筆資料，因此當資料量比較大時，會讓樹的高度變得很高。
這樣就不適合用在硬碟上(以上介紹的樹都適合用在記憶體中)，因為每一次與根節點比較數值大小時，就需要對硬碟進行一次I/O操作(硬碟速度比記憶體慢很多)，當樹高很高時，就意味著I/O次數也會很多，導致效率低落。
所以B樹就是為了處理儲存大量資料以及優化硬碟I/O的場景而出現，他允許每個節點存放不只一筆資料，以減少樹的高度，最常見的就是資料庫與檔案系統的應用。

定義

B樹是一種由二元搜尋樹延伸出來的m階搜尋樹。

  1. 每個節點有<=m個子節點
  2. 每個有k個子節點的非葉節點，有k-1個值
  3. 除非是空樹，不然Root根節點要有>=2個子節點
  4. 除了Root根節點與Leaf葉節點以外的節點，需滿足：⌈m/2⌉<子節點數量<=m
  5. 葉節點需要全部在同一層

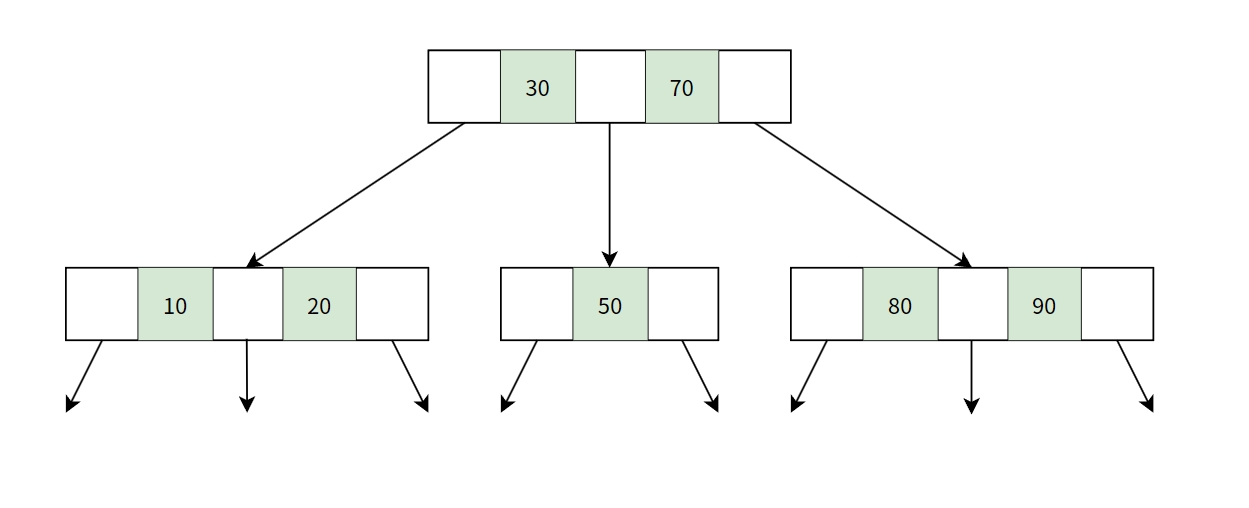
2-3樹 2-3-4樹

3階B樹因為每個節點可能會有2個或3個子節點，所以又被稱為2-3樹。
而4階B樹因為每個節點可能會有2、3或4個子節點，所以又被稱為2-3-4樹。

B+樹

B+樹是由B樹改良而來的，相較於B樹有以下優勢：

  1. 查詢速度穩定
  2. 容易做範圍搜尋
  3. 更少的I/O操作

B樹的缺點

首先我們要先了解，一般儲存資料時，都會有一個索引(Index)對應該資料實際的值，可以想像是每筆資料都有自己專屬的ID可以方便查詢。
所以在B樹中，我們的結構可能會長得像這樣：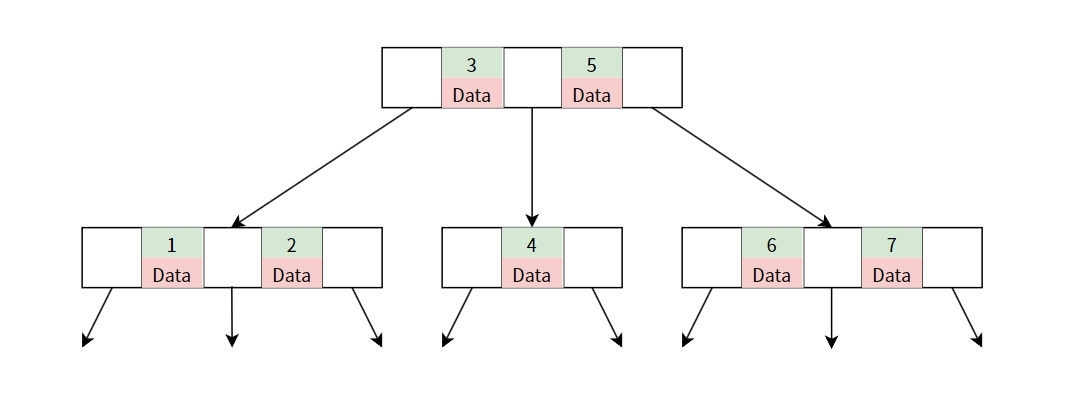

查詢不穩定

如果說我們今天要查詢Index=3的資料，我們可以在第一層就找到，但如果要查Index=1的資料就要在第二層才能找到，這就是查詢每筆資料時的不穩定。

不易做範圍查詢

如果說我們想要查Index>=2的資料，就需要走訪每個節點才可以找到，非常沒效率。

單筆資料比較大時I/O仍舊會很高

其實B樹在硬碟中，每個節點都會被分配4KB的空間可以儲存Index和資料，如果我們每筆資料大小比較小的話還好說，每個4KB節點空間就可以放下很多資料。
但如果每筆資料都很大，導致每個4KB的節點只能存放一筆資料的話，這樣節點數量就會隨之增加，進而影響樹高與I/O效率。

B+樹改善

B+樹將所有包含資料的節點全部移到葉節點，非葉節點只負責儲存Index，並且在葉節點之間建立鏈表，將資料都串連起來。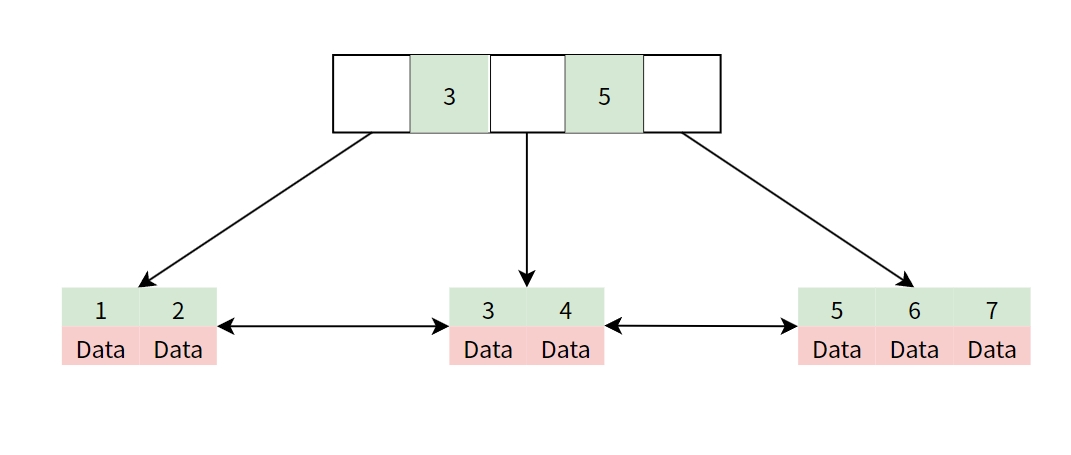

如此一來，就可以

  1. 查詢速度穩定
    因為所有資料都在葉節點，因此查詢任何資料都要查詢葉節點才可以找到，速度都是一樣的。
  2. 容易做範圍搜尋
    葉節點資料之間因為有鏈表，所以可以快速找到Index>=2的資料，而不用走訪每個節點，提升效率。
  3. 更少的I/O操作
    非葉節點只需要存放Index，因此可以在4KB的節點內存放更多Index，更節省節點數。

應用

MySQL的內核InnoDB就是使用B+樹儲存資料的。

結論

我自己之前在學習樹的時候，因為不知道樹到底可以做什麼、為什麼要用樹存資料、不同樹解決什麼問題，所以學習時很沒有方向，每次看完書後都還是一知半解。
而在這次參考許多資料及整理筆記後，讓我對樹有更全面的理解，了解到樹就是為了更快速查詢資料而出現的，不同種類的樹都有各自合適的應用場景，幫助我在面對各種與樹相關的知識不再那麼困惑，能用更深入的角度思考問題。

參考資料

書

資料結構 使用C++
圖解資料結構 使用Python

文章

維基百科-紅黑樹
Red-Black Tree / 紅黑樹
Linux 核心的紅黑樹
图解：什么是红黑树？

維基百科-B樹
B树和B+树详解
30-11 之資料庫層的核心 - 索引結構演化論 B+樹

其他

ChatGPT

__END__